まずデモ
デモを用意しました。マウスクリックで餌がおけます。ドラッグすることで餌の方向を指定できます。
生物っぽいルート計算とは🤔?
魚などの生物の群れの動きをシミューレーションするアルゴリズムではBoidsと言うものが有名ですね。お互いの位置関係のみで動く単純なアルゴリズムで非常に面白い動きをします。以下の動画がわかりやすいです。
www.youtube.com
しかし今回私が作りたいものは、これらとは違います。スタートとゴールの位置と向きを設定し、そのルートを生物っぽくなるように計算するというものです。
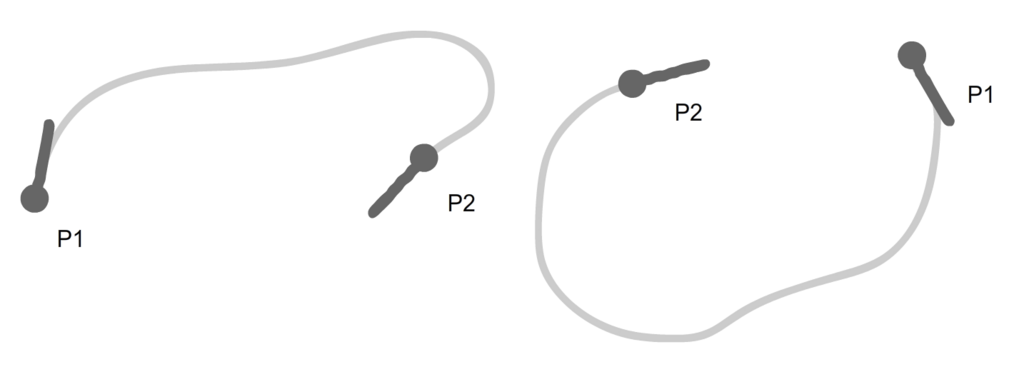
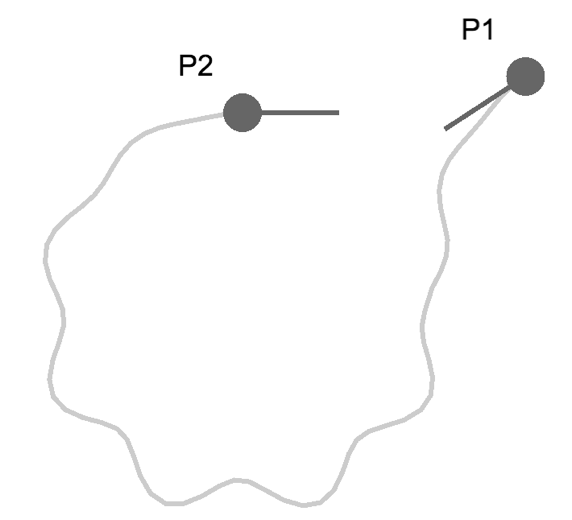
上の図は、私の思う、生物っぽいルートの手書きのイメージ図です、P1がスタート、P2がゴールです。この図を見て「その場で回転して方向を合わせてから進めば効率よくない?」「大回りしすぎじゃない?」「なんか、うねうねしてない?」と思う方がいると思います。
しかし、魚等の生物の場合その場で回転できないので、大回りをする必要があります。ただし、大型の魚の場合小回りがききません。また、生物は直線移動はしません。これらを踏まえて、ここで言う生物っぽさを定義します。
・その場で回転しない。
出来る生物もいるが、今回は無しとする。
・大回りしたりしなかったりする。
どれだけ小回りがきくかは生物の種による。
・完全な直線は描かない。
ちょっとうねうねしたりする。
私が勝手に超単純な条件を定義してしまいましたが、定義を複雑化するとアルゴリズムも大変になり、またそのライブラリを使うのも大変になります🤔 今回はこの条件で生物っぽさを表現したいと思います。
アルゴリズムの説明
小回り度
まず小回り度と言うものを定義しました。これは、その生物がどれだけ小回りがきくか?を示す値です。
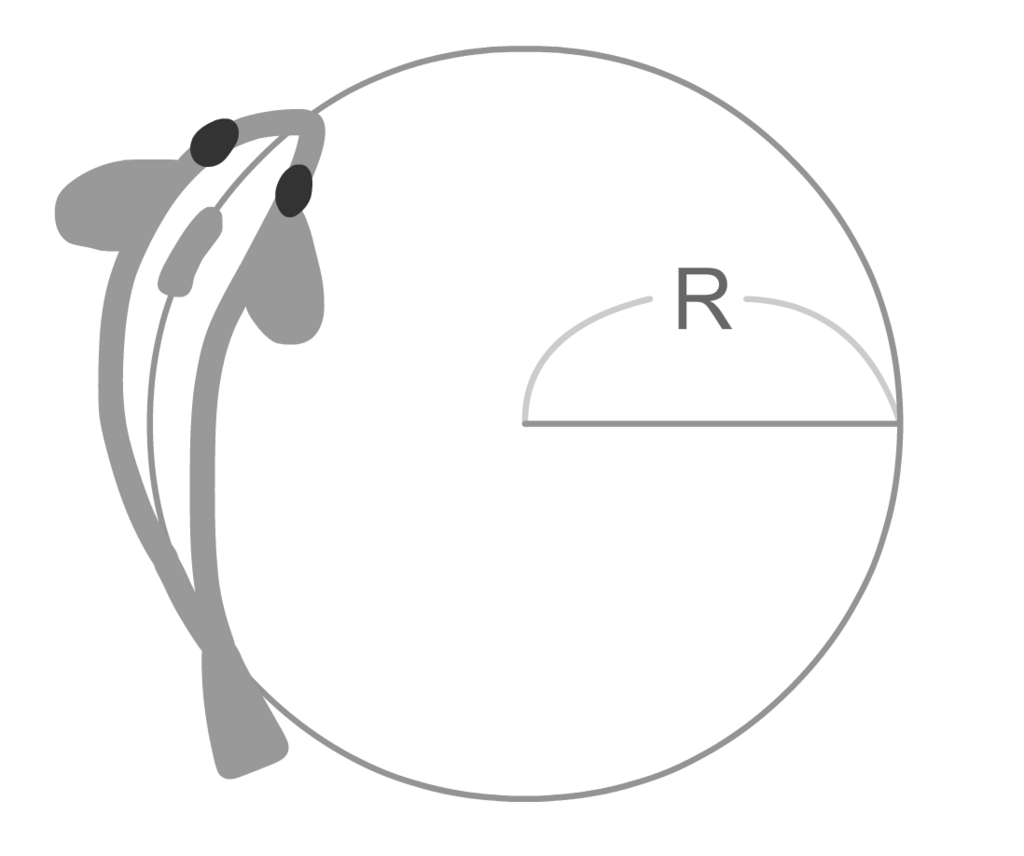
上の図は小回り度がRの魚の例です。この魚はターンで描ける最小の円の半径がRです。このRが小回り度です。この小回り度という概念がルート計算のミソです。
スタートとゴールに向きがある
はじめにも書きましたが、今回はスタートとゴールが位置のみではありません。位置と向きです。っぽさのの条件の1つとして、その場で回転できないと定義したので、スタートとゴールにも向きがなければなりません。
とりあえずスタートからゴールに移動するには
一旦、完全な直線を描かないという条件を捨てて、スタートからゴールへの、小回り度を満たすルート計算方法を考えてみます。
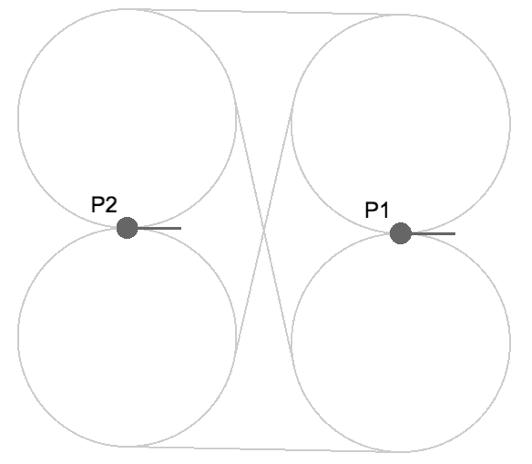
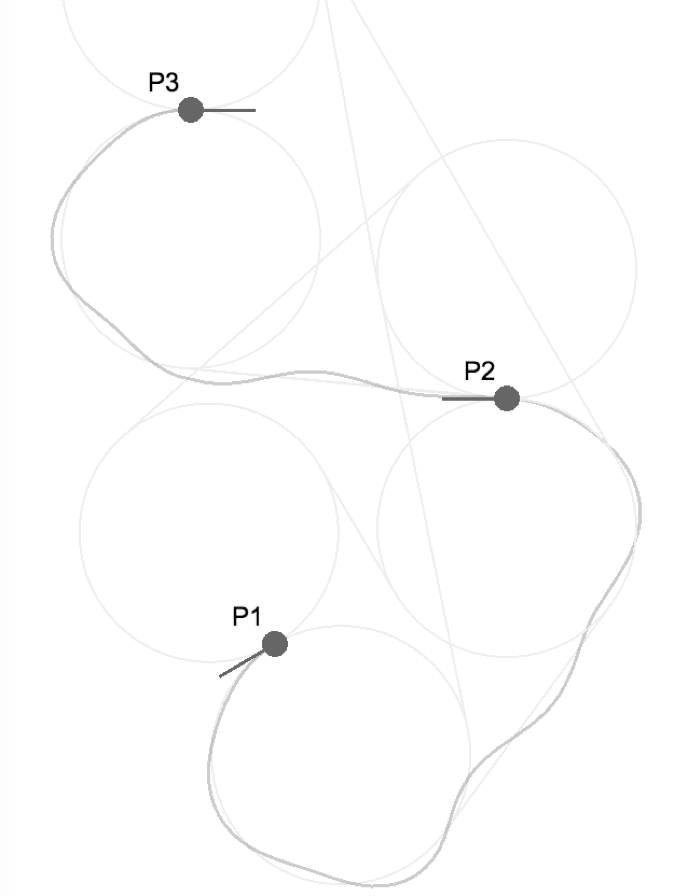
スタート(P1)とゴール(P2)、それぞれの位置からベクトルに対して±90度になる位置に円(半径は小回り度)を書きます。その円と円の必要な分の共通接線を書くと、上の図のようになります。更に、円の孤と接線をたどれば、小回り度を満たしつつP1がP2へたどり着くためのルートが見えてきます。
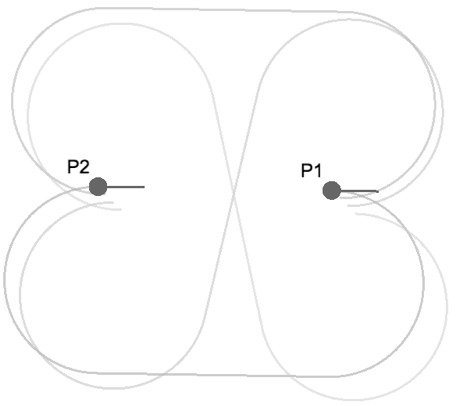
その方法で、実際にルートを書いてみました。重なってしまうので、ルートの線を少しずらしています。(見にくくてすみません)今回、ルートは全部で4つあるようです。共通接線の方法だと、ルートは最大で4つ、最低でも1つ生成されます。
わざとうねうねさせてみる
生物っぽい条件の中でまだ満たしていないのは、残りの完全な直線を描かないだけですね。
小回り度を満たすルートは生成できましたが、もちろんまだ生物っぽさが足りません。直線と正円の孤で生成されたルートは綺麗すぎます。強いて言うなら車っぽいでしょうか?
うねうねといえばsin、cosですね🤔。私は高校3年の最後の数学のテストを0点取るくらいには数学が苦手で、大学に入ってからちょっと手を出したくらいです。そんな私が「うねうねといえばsin、cosですね🤔」などと語る事をどうか許してください。誰でも最近知った言葉とか使いたくなりますよね?今私はそれです。
とりあえずまず直線に対してsinを適用してみる

まずP1からP2に移動するだけの直線ルートを用意しました。これをsinでうねうねにしてゆきます。
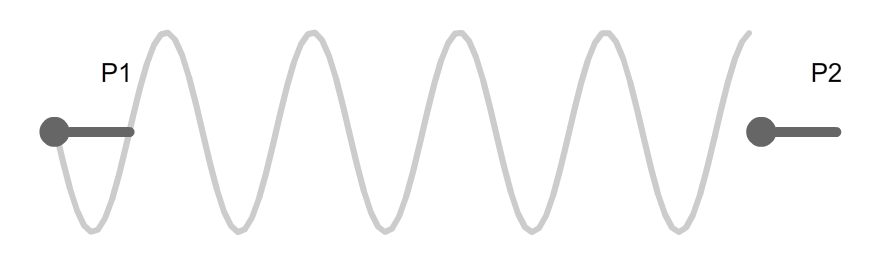
まず単純にベクトルに対し直角の方向へsinを適用しウェーブしました。しかし、うねうねのせいでP1のベクトルとずれてしまいました。また、P2に至ってはゴールがずれています。sinも使い方を気をつけないと、このように暴れてしまいます。
これらの2つの問題を同時に解決する方法を考えました。単純な方法です。これにさらに上から大きなcos(-π ≦ θ ≦ π)を掛けます。
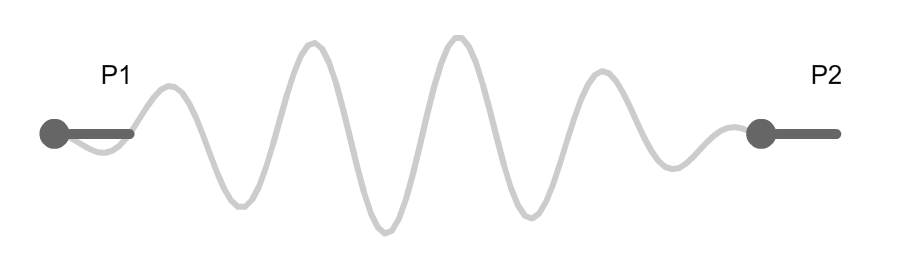
するとこうなります。sinでうねうねさせ、ルートの中間で遊びつつ、ちゃんとゴールへたどりつきます。
ついに完成...!
一言で言えば、小回り度によって書かれる円との共通接線と孤を利用したルートにsinとcosを与えただけです。以下の図は、こののアルゴリズムで生成したルートでのす。
虫っぽいルート
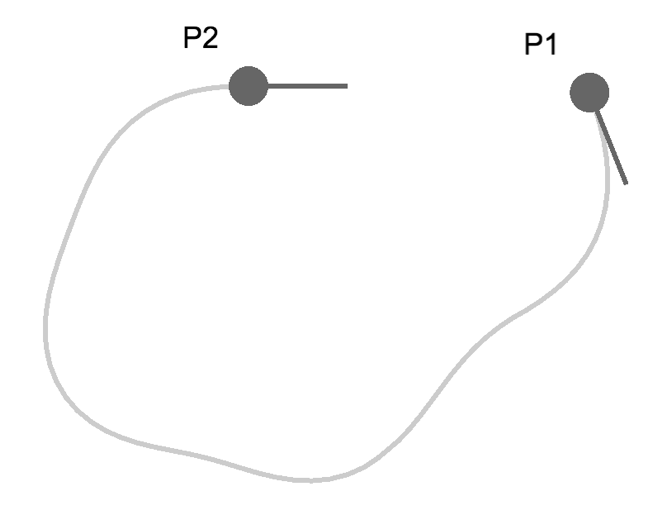
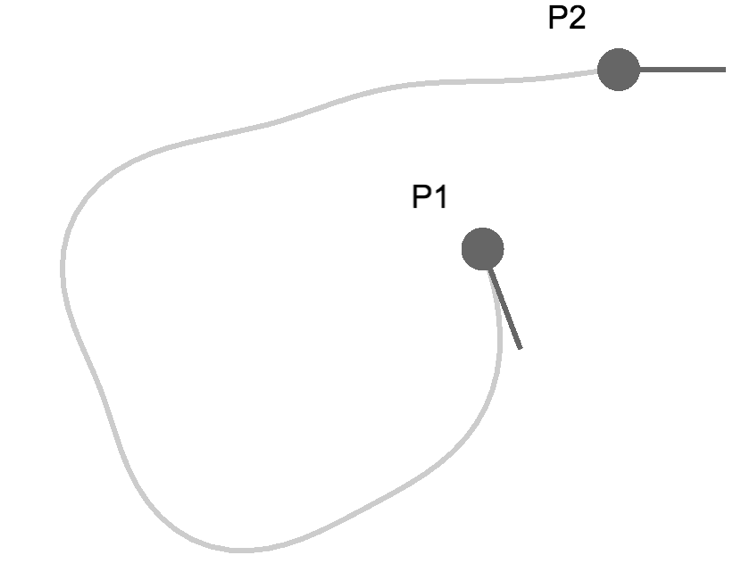
魚の泳ぐ感じのルート
中間点を設けたルート(補助線あり)
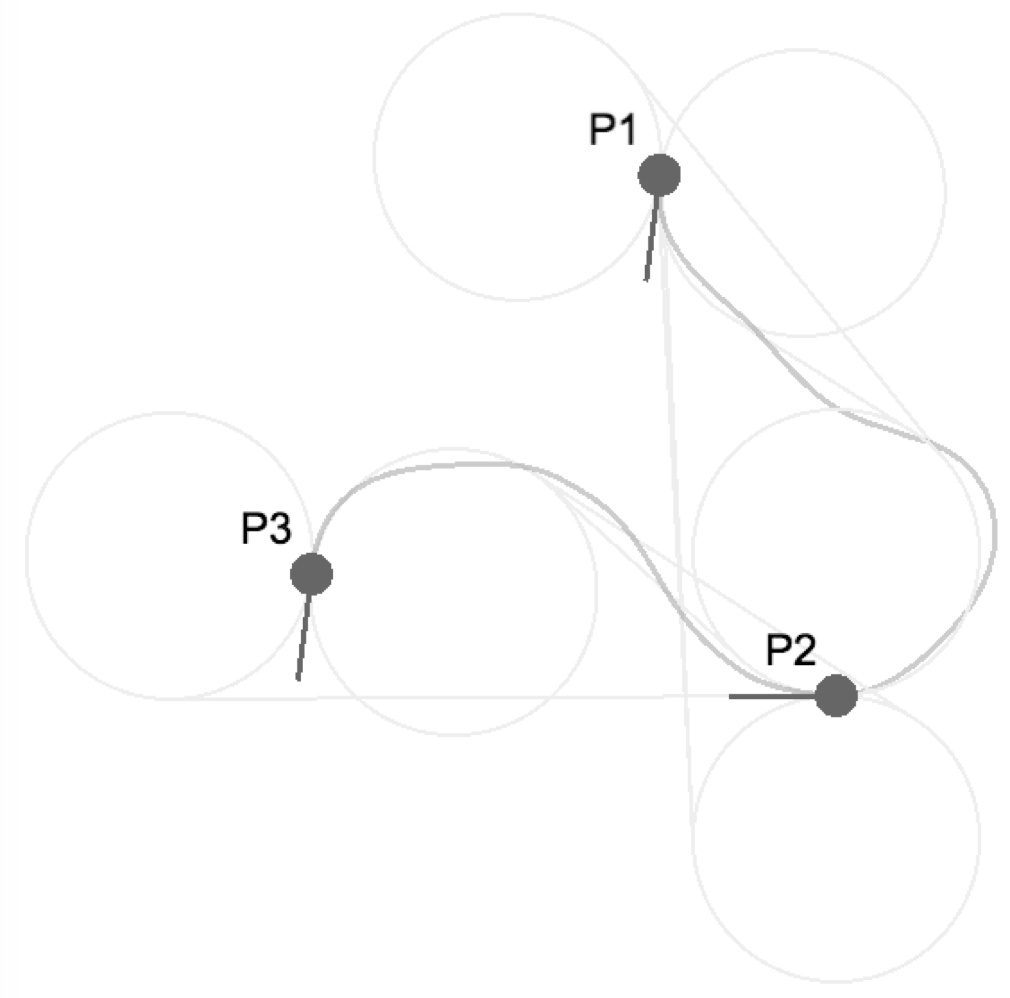
こんな感じです。どうでしょうか!生物っぽさを感じますでしょうか?
ライブラリ
このライブラリはTypeScript製です。JavaScriptかTypeScriptで使えます。次回の記事で、ライブラリの使い方とサンプルについて説明します。まだドキュメントもないので全く使い物になりませんが、一応おいておきます。 github.com
インストール
npm install routes @types/routes --save --registry http://npm.takumus.com